Llevo veinte años haciendo modelos de simulación dinámica. Se trata de formular sistemas de ecuaciones diferenciales que representan la variación en el tiempo de determinadas variables, como puede ser el nivel de un acuífero, el espesor de suelo fértil o el número de animales que vive en un territorio (por citar algunas con las que he trabajado). Hablo, por tanto, de modelos que generan trayectorias temporales.

Modelar consiste en seleccionar aquellas variables y procesos que resultan esenciales para explicar el comportamiento del sistema que se está estudiando. Ello obliga, ineludiblemente, a descartar ciertas variables y a prescindir de ciertos procesos. Hay autores que aseguran que hacer modelos matemáticos es un arte. Esa afirmación la encuentro un poco exagerada pero denota pasión por los modelos matemáticos, algo, es cierto, que no parece muy congruente. Me refiero a eso de poner en un mismo contexto pasión y ecuaciones diferenciales.

Sin embargo, en ciertas fases del modelado uno ha de dar rienda suelta a su creatividad. Esta es la parte buena del trabajo puesto que inventar cosas, en este caso un mecanismo explicativo de procesos como la desertificación o el cambio climático, siempre resulta una actividad satisfactoria.

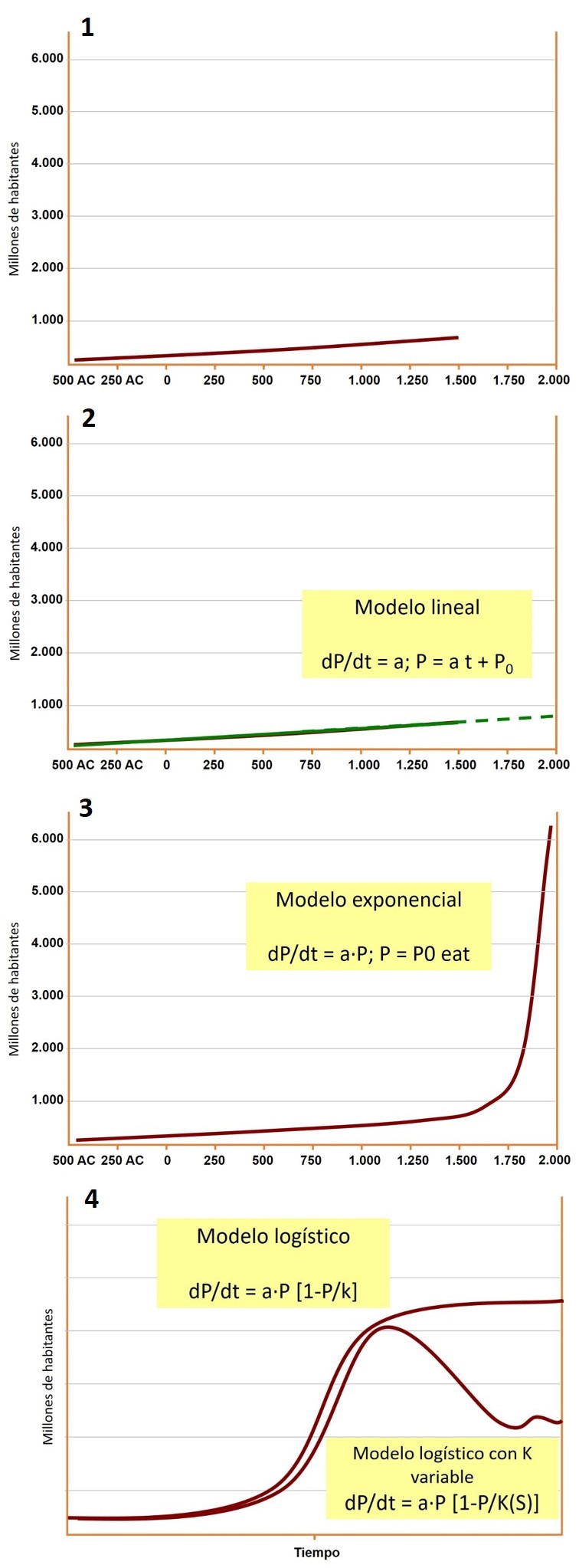Supongamos que en el año 1500 alguien se propone hacer un modelo para estimar la evolución de la población mundial y para ello cuenta con datos bastante precisos (1). Después de mucho pensar concluye que un modelo lineal permite encajar sus estimaciones con lo observado. Convencido de que el modelo está bien -los Supercicutas han dado su visto bueno- pronostica que en el año 2000 la población puede que llegue a los 1000 millones de habitantes (2).  Llegado el siglo XXI comprobamos con asombro que ese modelo estaba mal, de hecho, muy mal (3). La población supera los 6.000 millones de habitantes.

A medida que se progresa en la estructura de ecuaciones, se definen las variables operativas y se prueban distintas formulaciones, uno va acercándose a la pregunta incómoda que aguarda al final del camino. Allí se acaba la diversión. Parece como si unos sabios guardianes con muy mala leche, armados con porras y otros objetos contundentes, te estuviesen esperando para preguntarte: Sí, sí, muy bonito pero ¡¿ESTÁ BIEN ESE MODELO?!

Esa pregunta encierra cuestiones más específicas: ¿Tú modelo se parece a la realidad? ¿Hasta qué punto lo que dice tu modelo puede verificarse con datos REALES?

A mí me acojonaba llegar a ese Limbo y me enfrentaba con sudores a las escrutadoras miradas de los Supercicutas. Hasta que leí un paper que me hizo ver las cosas de otra manera. El título era contundente, Todos los modelos están mal y las explicaciones que seguían a un título tan provocador, muy claras y convincentes. Lo mejor es que no lo escribía un cualquiera, sino el mismísimo John Sterman, a la sazón el heredero en el MIT del inventor de la Dinámica de Sistemas. Vamos, un tipo que sabe de lo que habla.

El planteamiento de Sterman es bien sencillo. Los modelos son simplificaciones deliberadas de la realidad para poder entender ciertas partes de ese complejísimo entramado. Por tanto, cualquier modelo saldrá malparado de su comparación con la realidad. Es más, la obsesión por reproducir la historia, esto es, por ‘clavar’ los resultados del modelo con las observaciones, muchas veces actúa en detrimento de la calidad del modelo. Un ejemplo nos ayuda a ilustrar este punto.

¿Cómo es posible que un modelo que estaba bien dé unos resultados tan malos? La razón de fondo es que en el planteamiento del modelo se han ignorado las razones y mecanismos subyacentes. Es esencial, al plantear modelos, olvidarse un poco del pasado, de las observaciones, y centrarse en comprender el problema. Un comportamiento lineal puede ser el preludio de un crecimiento exponencial. Sin embargo, un modelo exponencial (no se ve bien en el gráfico, pero es Po por ‘e’ elevado a ‘a·t), que se ajustaría muy bien a los datos observados hasta el año 2000, tampoco funcionaría bien, puesto que estaríamos asumiendo que algo puede crecer de manera indefinida, violando las leyes de conservación de la masa.

Cuando se diseñan modelos hay que considerar las repercusiones más allá del rango habitual de comportamiento (hasta la fecha) de las variables estudiadas. En este caso un modelo logístico podría representar bien las futuras trayectorias de la población (asumiendo que se estabilizasen). Si, además, tenemos en cuenta la posibilidad del deterioro de la capacidad de carga del sistema el modelo sería más completo (4).

El problema para el que está únicamente pendiente de ajustar sus resultados a las observaciones (que a su vez pueden tener errores de medición o ponderación) es que a medida que introducimos mecanismos explicativos las trayectorias generadas las observaciones no replican exactamente las trayectorias que genera el modelo.

Dicho todo esto, la baza Sterman no exime de someter al modelo a una serie de pruebas que nos permitan comprobar su robustez y utilidad. En efecto, un modelo ha de evaluarse en función de su propósito. No podemos esperar pronósticos diarios de un modelo climático ni que un modelo meteorológico nos diga si va a llover el 26 de diciembre de 2025.

Esta evaluación, más completa, utiliza toda la información disponible, incluyendo las trayectorias pasadas de las variables que se estudien, las opiniones de expertos y la información blanda, esto es, de carácter cualitativo. Consiste en someter al modelo a preguntas impertinentes que le busquen las cosquillas. Se trata, por ejemplo, de saber si nuestro modelo da respuestas coherentes cuando se le saca de los intervalos habituales de funcionamiento, algo nada descabellado ante un contexto tan volátil como el actual (Cambio Climático, tecnología que cambia las cosas de la noche a la mañana, etc.). Un modelo que considere la producción agrícola debería dar una productividad nula en ausencia de agua. He estudiado algunos que muestran ajustes cojonudos en los intervalos de riego normales (500-3000 m3/ha/año) pero que siguen produciendo tanto si reciben 20.000 m3 (no se ahogan) o no les llega ningún aporte hídrico (en otras ocasiones he sido testigo de rendimientos negativos).

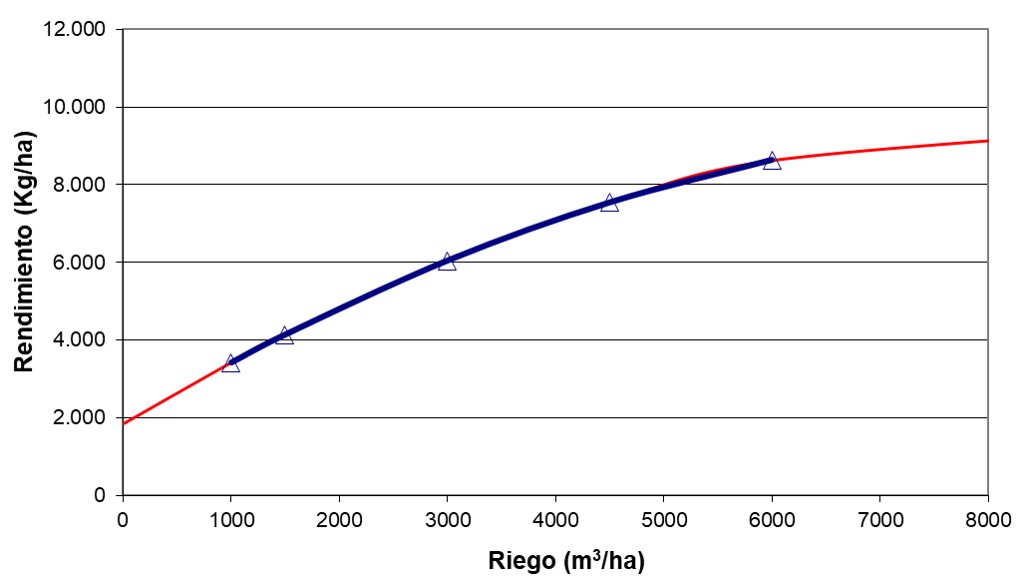
Ensayos de riego y rendimiento en trigo (triángulos). Modelo polinómico ajustado (línea azul). Respuesta del modelo ante eventos extremos (línea roja)

Comprobar la consistencia dimensional de las ecuaciones, documentarlas, realizar análisis de sensibilidad e implementar otros tests como los que propone este artículo aportan mucho más rigor a un modelo que simplemente se ciña a la bondad del ajuste con los datos observados.

Tomad nota Supercicutas.